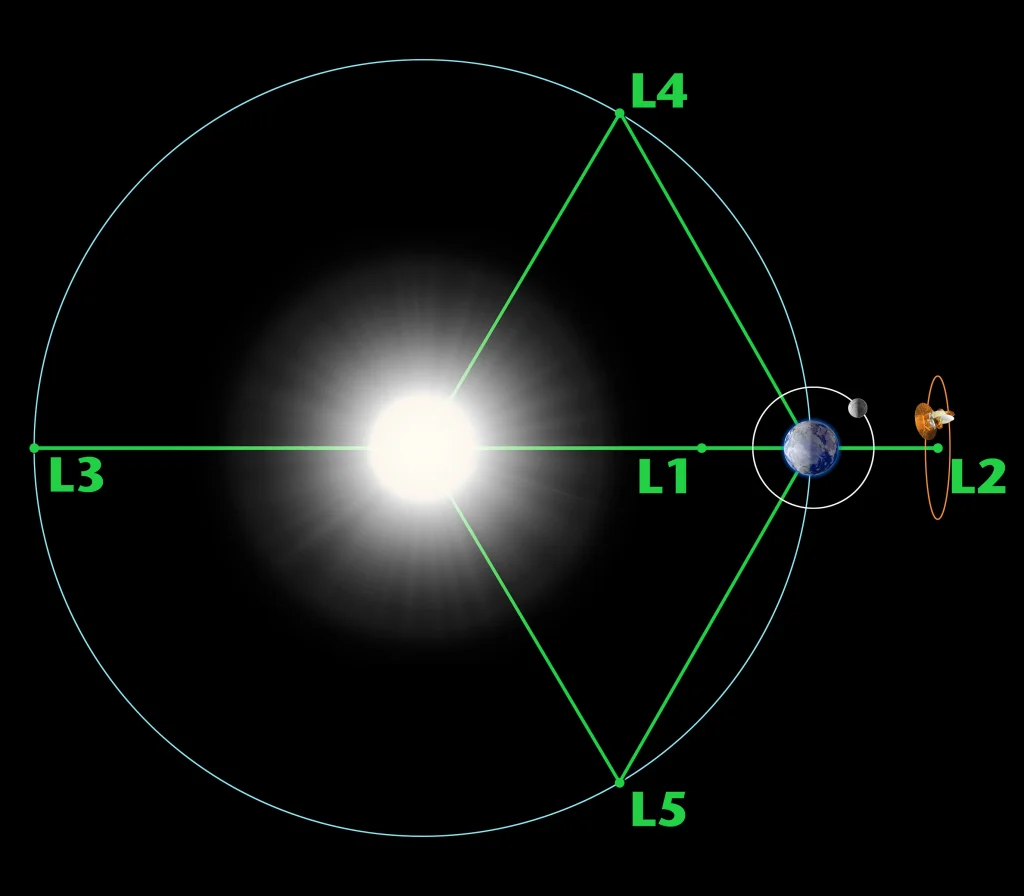
The Lagrange Points

/ Blog / By

The Lagrange points are specific points in space where the gravitational forces of two large bodies, like the Earth and the Moon or the Earth and the Sun, create a stable equilibrium with the centrifugal force of a smaller object placed at that point. There are five Lagrange points labeled L1 to L5 for any combination of two orbital bodies[1][2].

  • L1 Point: This point lies on the line between the two large masses where their gravitational attractions combine to produce equilibrium. Objects at this point have an orbital period equal to Earth’s orbital period and are about 1.5 million kilometers from Earth in the direction of the Sun[2].
  • L2 Point: Located on the line through the two large masses beyond the smaller one, at L2, the combined gravitational forces balance the centrifugal force on a body placed there. The James Webb Space Telescope is located at L2 to reduce light noise[2].
  • L3 Point: Also lying on the line through the centers of both large bodies but on the opposite side of one of them, L3 is another Lagrange point where gravitational forces balance out[3].
  • L4 and L5 Points: These points are symmetrically placed around the center line and at positions 60 degrees from it, forming vertices of equilateral triangles with the two large bodies. They are stable locations where objects can orbit without drifting away[2].

In summary, Lagrange points are locations in space where gravitational forces create a stable equilibrium, allowing objects to maintain their position relative to two larger bodies.

Citations:

[1] https://en.wikipedia.org/wiki/Lagrange_point
[2] http://datagenetics.com/blog/august32016/index.html
[3] https://www.spaceacademy.net.au/library/notes/lagrangp.htm
[4] https://www.sciencedirect.com/topics/engineering/lagrange-point

Here is a function to calculate the Lagrangian points between two masses [in Python]:

import numpy as np
G = 6.67e-11 # Gravitational constant
def lagrange_points(m1, m2, r):
"""
Calculate the Lagrangian points between two masses m1 and m2 separated by distance r.
Parameters:
    m1 (float): Mass of primary object 
    m2 (float): Mass of secondary object
    r (float): Distance between m1 and m2

Returns:
    x1, x2, x3, x4, x5 (array): Positions of the 5 Lagrangian points
"""

# Mass ratio
mu = m2 / (m1 + m2)

# Lagrangian point positions are given by:
x1 = r * (1 - mu) 
x2 = r * (1 + mu)
x3 = 0
x4 = -r * np.sqrt(mu)
x5 = r * np.sqrt(mu)

return np.array([x1, x2, x3, x4, x5])

To use it:

m1 = 1e30 # Mass of Earth in kg
m2 = 3.3e23 # Mass of Moon in kg
r = 3.84e8 # Distance between Earth and Moon in m

points = lagrange_points(m1, m2, r)

print(points)

This will calculate and return the positions of the 5 Lagrangian points between Earth and Moon masses separated by their average distance.

Note:

After reading several articles about Lagrange points, I decided to take notes on the topic and shared them here to keep a record.

Sources:

Updated in December 2022